
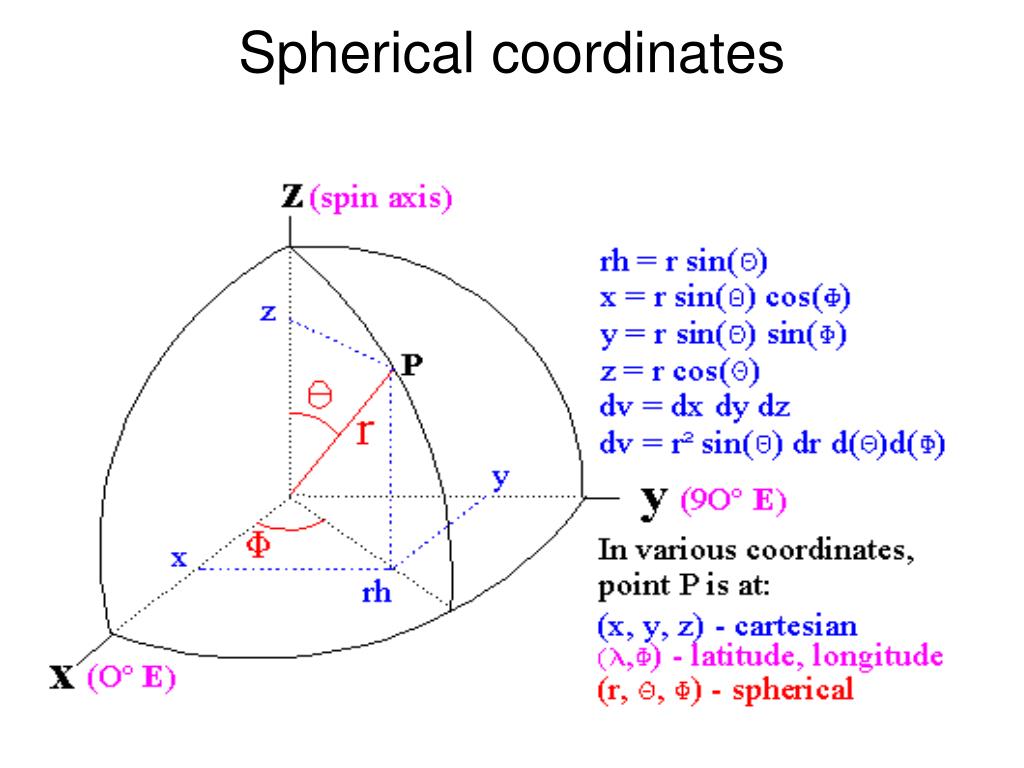

is the angle between the projection of the radius vector onto the x-y plane and the x axis. I'll highlight the most common sources of errors and I'll show an alternative proof later that doesn't require any knowledge of tensor calculus or Einstein notation. The basis vectors are tangent to the coordinate lines and form an orthonormal basis er,e,e e r, e, e that depends on the current position P P. Given two vectors whose initial point is the origin of a system of spherical coordintes and terminal points P1(1,1,1) P 1 ( 1, 1, 1 ) and point P2(2. Youd basically need to create a class for spherical that has this same functionality. Vector fields in cylindrical and spherical coordinates. You asked for a proof from "first principles". Spherical Coordinates (r ) In spherical coordinates, we utilize two angles and a distance to specify the position of a particle, as in the case of radar measurements, for example.


 0 kommentar(er)
0 kommentar(er)
